
#Naca airfoil generator matlab code
Modificationsįour- and five-digit series airfoils can be modified with a two-digit code preceded by a hyphen in the following sequence: Finally, constant k 1 is determined to give the desired lift coefficient for camber-line 230 again, k 1 = 15.957 is used. The constant m is chosen so that the maximum camber occurs at x = p for example, for the 230 camber-line, p = 0.3 / 2 = 0.15 and m = 0.2025. Where the chordwise location x and the ordinate y have been normalized by the chord. The camber-line is defined in two sections:
Fourth and fifth digits give the maximum thickness of the airfoil (as per cent of the chord).įor example, the NACA 12018 airfoil would give an airfoil with maximum thickness of 18% chord, maximum camber located at 10% chord, with a lift coefficient of 0.15. Second and third digits, when divided by 2, give p, the distance of maximum camber from the leading edge (as per cent of chord). The first digit, when multiplied by 0.15, gives the designed coefficient of lift (C L). The NACA five-digit series describes more complex airfoil shapes: p is the location of maximum camber (10 p is the second digit in the NACA xxxx description).įor this cambered airfoil, the coordinates ( x U, y U) and ( x L, y L), of respectively the upper and lower airfoil surface, become:. m is the maximum camber (100 m is the first of the four digits),. The formula used to calculate the mean camber line is: The simplest asymmetric foils are the NACA 4 digit series foils, which use the same formula as that used to generate the 00xx symmetric foils, but with the line of mean camber bent. Plot of a NACA 2412 foil, including camber line and thickness Now the coordinates ( x U, y U) of the upper airfoil surface, and ( x L, y L) of the lower airfoil surface are: Equation for a cambered 4-digit NACA airfoil The leading edge approximates a cylinder with a radius of: to -0.1036) will result in the smallest change to the overall shape of the airfoil. If a zero-thickness trailing edge is required, for example for computational work, one of the coefficients should be modified such that they sum to zero. Note that in this equation, at (x/c) = 1 (the trailing edge of the airfoil), the thickness is not quite zero. t is the maximum thickness as a fraction of the chord (so 100 t gives the last two digits in the NACA 4-digit denomination). y is the half thickness at a given value of x (centerline to surface), and. x is the position along the chord from 0 to c,. The formula for the shape of a NACA 00xx foil, with "xx" being replaced by the percentage of thickness to chord, is: Plot of a NACA 0015 foil, generated from formula 
Equation for a symmetrical 4-digit NACA airfoil The 15 indicates that the airfoil has a 15% thickness to chord length ratio: it is 15% as thick as it is long. The NACA 0015 airfoil is symmetrical, the 00 indicating that it has no camber.
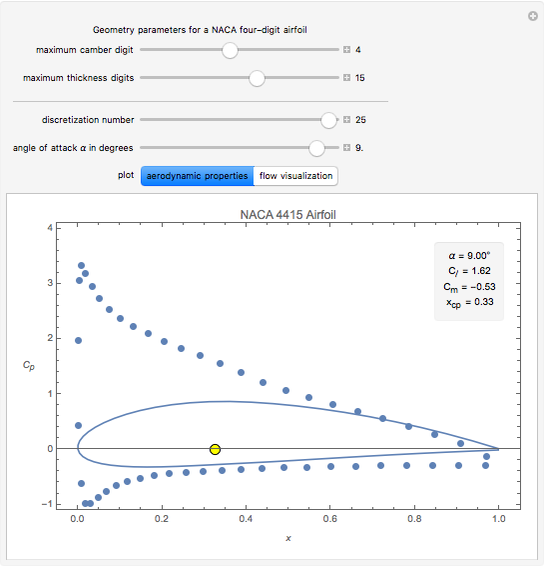
Four-digit series airfoils by default have maximum thickness at 30% of the chord (0.3 chords) from the leading edge. Two digits describing maximum thickness of the airfoil as percent of the chord.įor example, the NACA 2412 airfoil has a maximum camber of 2% located 40% (0.4 chords) from the leading edge with a maximum thickness of 12% of the chord.One digit describing the distance of maximum camber from the airfoil leading edge in tens of percent's of the chord.One digit describing maximum camber as percentage of the chord.The NACA four-digit wing sections define the profile by: 1.2 Equation for a cambered 4-digit NACA airfoil.

1.1 Equation for a symmetrical 4-digit NACA airfoil.







 0 kommentar(er)
0 kommentar(er)
